「量学堂-16」假设检验(中)
时间:2017-07-19 来源:互联网 浏览量:
接着我们上一篇继续,没看前一篇的同学可以看我以前发布的文章 “「量学堂-15」假设检验(上)”。
让我们先获取股价数据:
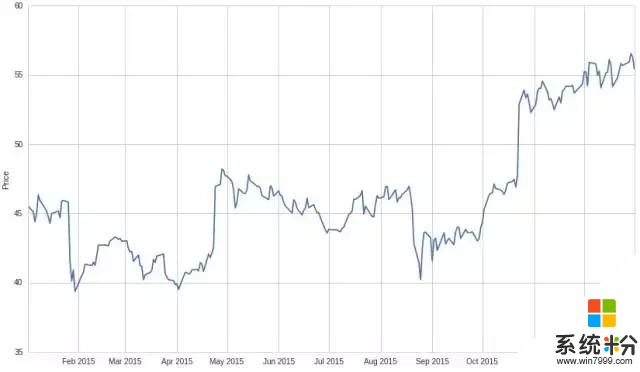
将其转换为日收益率:

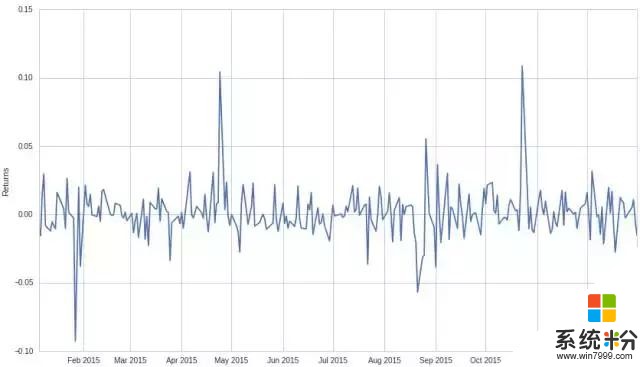
这里不知大家是否有这样的疑问,既然我们的“原假设(虚无假设)”与“替代假设”分别为:H0:微软股价收益率的均值为 0;HA: 微软股价收益率的均值不为 0。那为什么我们不直接算得微软的股价收益率均值,从而来直接检验假设的正确性呢?
因为我们无法获得完整的总体数据(每天都会产生新的股价,生生不息),而是只能获得某个有限时间段内的收益率样本。我们并不确定样本是否可以反应总体的情况。正是由于这种不确定性,我们才需要使用统计检验。
下面,我们选择合适的检验统计量以及对应的概率分布。检验统计量通常采用以下的形式:

检验统计量依靠样本数据计算出来,再与它的概率分布进行对比,来决定拒绝还是接受原假设。由于我们要检验的是微软股票的平均收益率是否为0,我们可以使用样本均值
作样本统计量。在已知总体标准差
时,通过
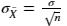
计算样本统计量的标准差;若总体标准差未知时, 通过
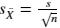
计算样本统计量的标准差,这里的 s 是样本标准差。根据假设,分子“基于原假设的总体参数值”指的就是“微软股价均值为0”,因此我们的检验统计量的计算公式可转化为:
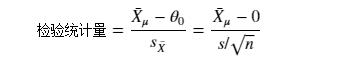
下面是四个最常用检验统计量及其分布:
t-分布 (t-检验)
正态分布 (z-检验)
卡方分布 (卡方-检验)
F-分布 (F-检验)
之后我们会具体展开。就目前而言,我们尝试在微软的例子中应用 z-检验。
选定了合适的检验统计量以及概率分布后,我们需要指定检验的显著性水平 α 值,拿它与我们的检验统计量比较,从而决定是接收还是拒绝原假设H0。
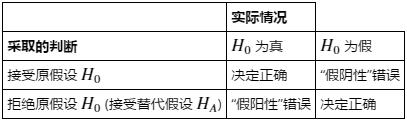
我们的显著性水平 α =“假阳性”错误发生的概率(“假阳性”是指:错误地判断H0不成立,实际H0 为真)。另一方面,我们把“假阴性”错误发生的概率记作 β (错误地判断 H0 成立,实际 H0 为假)。
如果我们试着减少“假阳性”错误发生的概率,我们将会增加“假阴性”错误发生的概率,反之亦然。同时减少两种错误发生的概率的唯一方式,就是增加样本容量。
常用的显著性水平 α 值有:0.1, 0.05 和 0.01。若 α = 0.1 的情况下拒绝原假设(虚无假设),意味着我们有某种证据显示原假设是错误的。若 α =0.05 时拒绝原假设(虚无假设),说明我们有充分的证据显示原假设是错误的,而当 α =0.01 时拒绝原假设,说明我们有着极其充分的证据显示原假设是错误的。
临界值
现在我们来寻找临界值,又称为“拒绝临界点”。我们将检验统计量与临界值进行比较,从而决定是否拒绝原假设。如果我们拒绝,我们称这种情况为“统计上是显著的”,如果我们不能拒绝原假设,则称之为“统计上不显著”。
我们根据假设检验的显著性水平阿尔法及其分布来决定检验临界值 ,在本例中,假设 α = 0.05,则我们的显著性水平就是 0.05。有两种设定临界值的方式来应用单边 z-检验:
如果我们检验 H0: θ ≤ θ0,HA: θ > θ0,显著性水平 α = 0.05,我们根据临界值0.05查对应的Z分布表得到 z0.05 = 1.645。再将检验统计量 z' 与 z0.05 比较,如果 z' > 1.645,我们拒绝原假设。
如果我们检验的是 H0: θ ≥ θ0,HA: θ < θ0 ,显著性水平 α = 0.05,我们同样查对应的Z分布表得到临界值 -z0.05 = -1.645。如果 z' < -1.645,我们将会拒绝原假设。
应用双边检测则会有些许不同。由于是“双边”,因此将有两个临界点,正值和负值。我们的 α = 0.05,因此假阳性发生的概率之和要是0.05,对于双边检验的情况,我们将 0.05分成“一半一半”,我们将正、负临界点分别记作 z0.025 和 -z0.025,对照分布表得到临界值分别为 1.96 和 -1.96。这种情况下,如果 z' < -1.96 或者 z' > 1.96,我们就拒绝原假设。而如果 -1.96≤ z' ≤ 1.96,我们则接受原假设。
当进行假设检验的时候,你也可以使用 P-值 来进行判断。P-值 是你可以拒绝原假设的最小显著性水平。人们经常把 P-值 理解成“原假设是错误”的概率,这是一种误解。P-值 只有在与显著性水平比较时才有意义。如果 P-值 < α ,我们将拒绝原假设,否则我们接受原假设。注意:更小的 P-值 并非意味着统计意义上更显著。有许多统计工具能够为你计算P-值,当然你也可以手工计算。计算规则取决于你的假设检验类型以及累计密度函数。如果要手工计算P-值,应遵循下述方法:
*对于“≤”的假设检验,P-值 = 1-累积密度值(检验统计量)
*对于“≥”的假设检验,P-值 = 累计密度值(检验统计量)
*对于“≠”的假设检验,P-值 = 2 * (1 - 累计密度值) (检验统计量)
未完待续
相关资讯
- 「最美应用」Groove:用微软家的这款音乐app听歌,我想怀疑人生
- 安卓之父也开始做音箱了;微软保罗·艾伦造出最大飞机用来发射火箭 | 一周「硬」资讯
- AMD推桌面CPU Ryzen ThreadRipper 16核32线程
- 「Microsoft bing」微软必应精选1,HD超清壁纸
- Unreal Engine虚幻引擎最新版本4.16发布
- 微软小冰全球项目负责人李笛揭秘:小冰如何成为写诗达人?
- 在微软与英特尔等巨头的助力下,Makeblock 要全方位布局「撬开」教育市场 | STEAM 教育特稿
- 勒索病毒上班日第二波攻击?工程师笑提「微软阴谋论」
- 必须知道:「勒索病毒」除了入侵微软电脑也攻击安卓、苹果手机
- 微软5月16日展开“Xbox向后兼容游戏大促销”:超过275款游戏加入此活动
